数论

质数

会一个线性筛法就可以了

primes = []
cnt = 0
st = [False] * 1000000

def get_prime(n):
    for i in range(2,n+1):
        if st[i]==False:
            primes.append(i)
        j= 0
        while(primes[j]*i<=n):
            st[primes[j]*i] = True
            if i%primes[j]==0: 
                break
            j += 1

get_prime(100)
print(primes)

欧几里得算法

def gcd(a,b):
    while b:
        a,b = b,a%b
    return a

def gcd2(a,b):
  return a if b==0 else gcd2(b,a%b)

质因数分解

每个数都可以表示为质数的乘积 $n=p_1^{k_1}*p_2^{k_2}*...*p_m^{k_m}$

题目: 给定 n 个正整数, 求它们乘积的约数的个数 $0<n<100$$a_i<10^9$

约数

约数的个数

如果一个数 $n$ 的质因数分解为 $p_1^{k_1}*p_2^{k_2}*...*p_m^{k_m}$, 那么它的约数个数为 $(k_1+1)*(k_2+1)*...*(k_m+1)$.

约数的和

如果一个数 $n$ 的质因数分解为 $p_1^{k_1}*p_2^{k_2}*...*p_m^{k_m}$, 那么它的约数的和为 $(p_1^0+p_1^1+...+p_1^{k_1})*(p_2^0+p_2^1+...+p_2^{k_2})*...*(p_m^0+p_m^1+...+p_m^{k_m})$.

欧拉函数

在数论中, 欧拉函数 $\phi(n)$ 是小于等于 n 的正整数中与 n 互质的数的个数.

如果一个数 $n$ 的质因数分解为 $p_1^{k_1}*p_2^{k_2}*...*p_m^{k_m}$, 那么它的欧拉函数为 $\phi(n)=n*(1-\frac{1}{p_1})*(1-\frac{1}{p_2})*...*(1-\frac{1}{p_m})$.

欧拉定理

如果 $a$ 和 $n$ 互质, 那么 $a^{\phi(n)} \equiv 1 \mod n$. 举例: a=5,n=6, $\phi(6)=2$, $5^2 \equ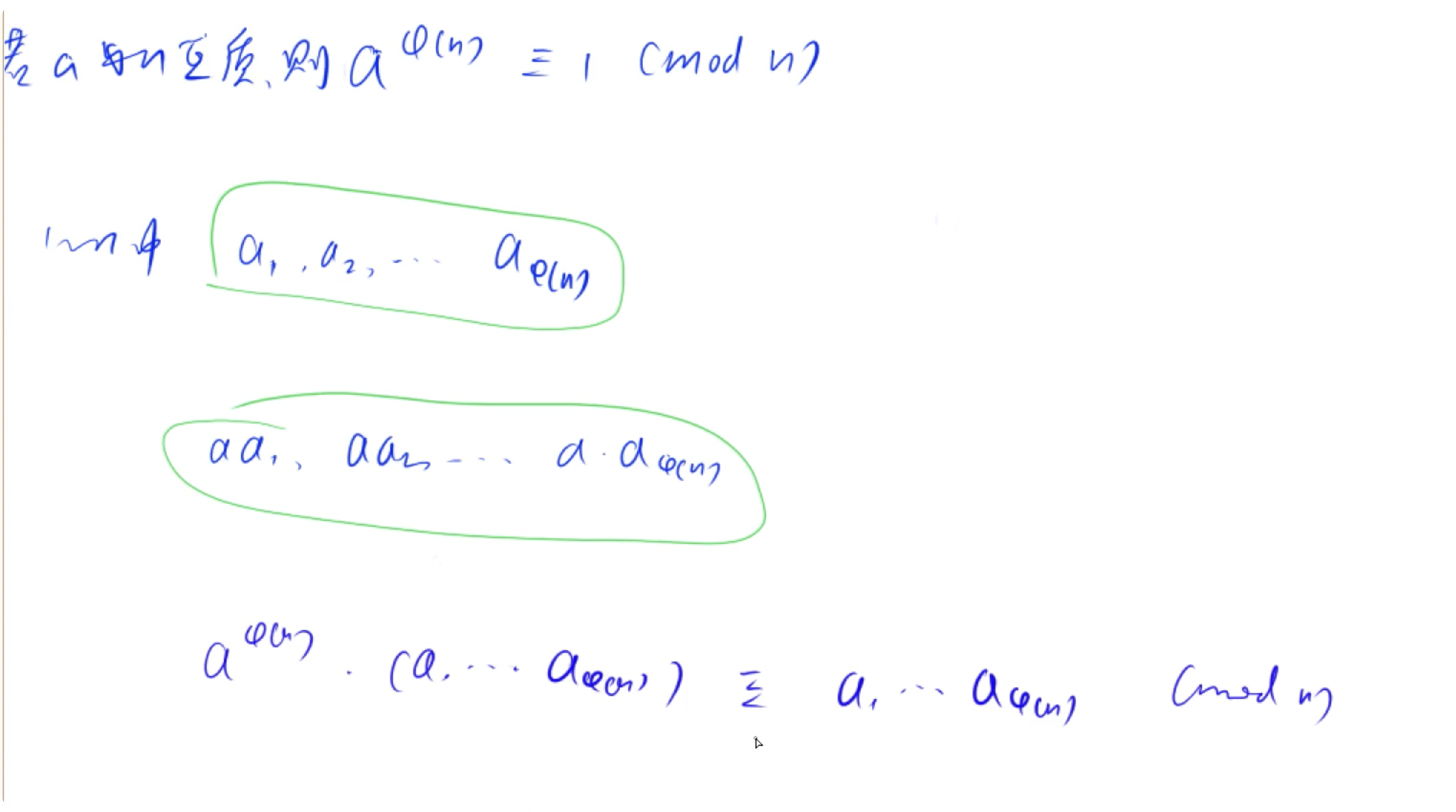iv 1 \mod 6$.

datetime

依据年,月,日 来创建日期对象

from datetime import date
d = date(2023, 3, 31)
print(d) # 2023-03-31

日期的偏差

timedelta

from datetime import date, timedelta
d = date(2023, 3, 31)
print(d + timedelta(days=1)) # 2023-04-01
t = timedelta(days=1,hours=1,minutes=1,seconds=1) # 1 day, 1:01:01
print(t.total_seconds()) # 90061.0
print(t.days) # 1
print(t.seconds) # 3661 可以得到所有的秒数

杂项

将字符转换为整数

ord

ord('a') # 97
ord('A') # 65

将整数转换为字符

chr

chr(97) # 'a'
chr(65) # 'A'

四舍五入

round

round(1.5) # 2